gamma(), gamma_r(), gammaf(), gammaf_r()

Log gamma function

Synopsis:

#include <math.h>

double gamma( double x );

double gamma_r( double x,
                int* signgam);

float gammaf( float x );

float gammaf_r( float x,
                int* signgam);

Library:

libm

Description:

The gamma() and gamma_r() functions return the natural log (ln) of the gamma() function and is equivalent to lgamma(). These functions return ln|Gamma(x)|, where Gamma(x) is defined as follows:

For x > 0:

For x < 1:

n / (Gamma( 1-x ) * sin( nx ))

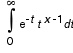
(The results converge when x is between 0 and 1.)

The gamma math function has the property G(N) = G(N-1)*N (it grows fast, so that's why log is used).

     lgamma(x) = ln (lgamma(x)) = gamma(x)

The lgamma() and lgammaf() functions use the external integer signgam to return the sign of Gamma(x) while lgamma_r() and lgammaf_r() use the user-allocated space addressed by signgamp.

The signgam variable isn't set until lgamma() or lgammaf() returns. For example, don't use the expression: g = signgam * exp( lgamma( x )); to compute g = Gamma(x)'. Instead, compute lgamma() first: lg = lgamma(x); g = signgam * exp( lg );

Note that Gamma(x) must overflow when x is large enough, underflow when -x is large enough, and generate a division by 0 exception at the singularities x a nonpositive integer.

Returns:

The gamma math function.

Classification:

Legacy Unix

See also:

lgamma()